本帖最后由 宇生人 于 2020-5-8 15:33 编辑
在太阳或行星的引力中行星或卫星之间 吸引与分离的初级估算解析 摘 要: 两颗行星相会(下合)它们彼此吸引,实质上这时在它们之间就有了一个微弱的质量中心存在,彼此就有一定的质量被这个质量中心所带来的状态驱动。对彼此参与到这个质量中心来的质量来说,太阳对它们在各自的星体上单独的引力之和与它们在两颗行星质量中心的引力之和的差与两颗行星的吸引力有着密切的关系。是一种潮汐现象,差值大于引力,两颗行星会显示出分离状态,差值小于引力,两颗行星会显示出吸引状态。共振与进动可能都与这有关系,还有轨道变迁等。 关键词:质量中心 参与质量 球体圆 地—月系统 潮汐现象 注释:本文所有的计算都是估算、简算,不可引用。 分类号:P 月球和地球有一个共同的质量中心,对太阳来说它们围绕着这个质量中心旋转成为一体。但这个质量中心不会突然出现。不管俘获说也好分离说也好这个质量中心是逐渐出现的。这里按俘获说讲,在将要俘获还没有完全俘获的时候太阳怎样吸引它们?不能按一个质量中心、一体算,象现在的地—月系统。也不能按两个质心、两体算,类似行星相会(下合)。通常计算地球、月球绕太阳公转轨道是按它们的质量中心算比单独算更准确 file:///C:/Users/ADMINI~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.gif。那么这时候实质上是两种因素都有,就要按照两种因素各自的包含量去分别处理。 两颗行相会它们彼此有吸引力,它们就有了相关性,就有了一个微弱的质量中心存在,就有了一点一体的因素存在,处理这个微弱的质量中心所带来的问题就是本文要讲的。
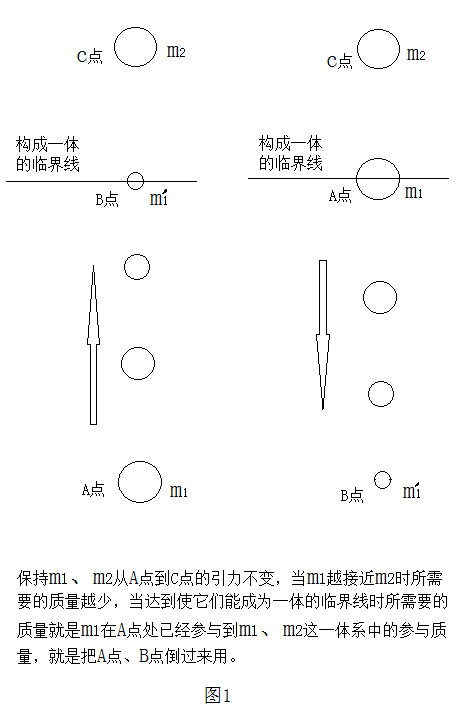
两颗行星互不相关时和相会时太阳对它们的引力是不同的,不是因为它们互相吸引了不同,而是因为有了这个微弱的质量中心了而不同。行星之间这个微弱的质量中心是实在存在的,计算的时候要用到它。两颗行星没有完全形成质量中心但形成了一小点,这就会改变太阳对这两颗行星的引力,并通过这个微弱质量中心把这个引力对两颗行星做二次分配,类似于地球上的潮汐现象。行星的运动主要是太阳控制,它们自身的引力作用很小,处于被动状态。
 地球上的物质是靠引力维持在一起的,不是象铁球、石球是靠粘合在一起的。地-月系统也是靠引力维持的,在这点上它们等效。地球只有一个质心,地-月系统有两个质心和一个共同的质量中心,那么太阳、地球、月球在一条直线上连珠时,地球和月球是不是象两颗行星相会呢?实质上两颗行星相会就有淡淡的这种因素存在,用类似于处理地-月系统问题的方法去处理两颗行星相会是我们要讨论和在理论上验证的。
地球上的物质是靠引力维持在一起的,不是象铁球、石球是靠粘合在一起的。地-月系统也是靠引力维持的,在这点上它们等效。地球只有一个质心,地-月系统有两个质心和一个共同的质量中心,那么太阳、地球、月球在一条直线上连珠时,地球和月球是不是象两颗行星相会呢?实质上两颗行星相会就有淡淡的这种因素存在,用类似于处理地-月系统问题的方法去处理两颗行星相会是我们要讨论和在理论上验证的。 这里还要说一个问题,引力的本质是什么?星体与星体之间的引力是怎么交换的?是在它们中间还是存在速度?还是象爱因斯坦说的时空弯曲?这还有待于研究。那么既然还没有定论我们就要重视现象的处理、计算方法的实用性。如果计算的结果与实测能吻合,则有利于解决实际问题和进一步研究引力的性质。处理两个星体之间的引力这好办,一对一就完事。处理三个星体之间的引力(三体问题)不宜再用一对一再一对一,再再一对一去处理,这里就涉及到它们之间的引力是怎么交换的问题,是怎么叠加的,叠加以后是怎么交换的?在哪个位置交换等。基于此,这里提出了这种处理星体之间引力作用的方式,估算结果与实际观测结果有吻合的趋势。本文提到的三个星体是:太阳和相邻的一颗内轨行星与一颗外轨行星,并且它们之间的距离是:两颗行星的间距小于内轨行星到太阳的距离。这样能行成一个条件:两颗行星先形成一个质量中心然后再对太阳而言。行星和卫星也是这样的条件。
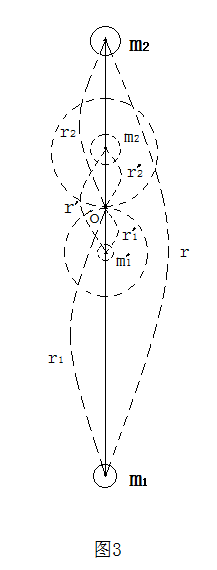
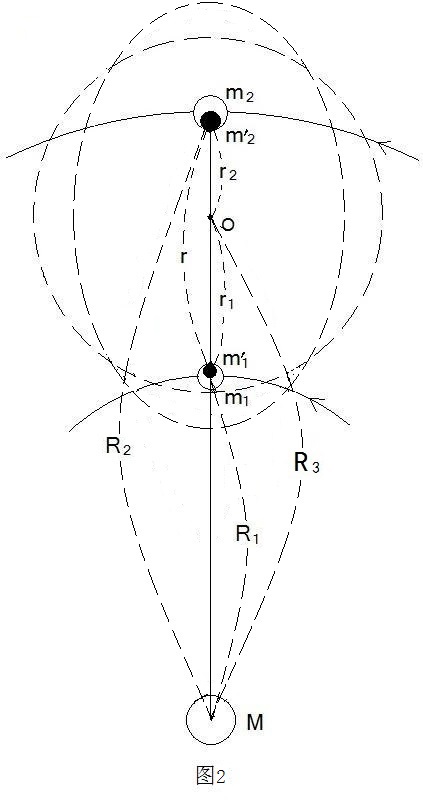
再说明一个问题,这里都是按质点计算,所以就是个位置、引力差、质量中心、参与质量的问题,并且是估算,暂时不必要考虑速度、离心力、平衡等细节问题,也不用考虑椭圆轨道和轨道倾角的事。这里相当于把两个行星互不相干的时候的状态叠加到一起后研究它们的引力关系。它们原本的质量、引力、离心力都是处于平衡状态,这里也就是即时的。主要是分析行星间这种吸引与分离是否存在的可能性,不是细究它们的运动状态。细究它们的运动状态是另外的课题。 如图1, m1、m2 的引力为:F,保持这个引力F不变,m1 为变量,则m1越接近m2所需要的质量越少,达到它们能成为一体的临界线时所需要的质量为m’1,把m1、m’1 的位置倒过来排,就是把A点B点倒过来,则m’1就是m1在A点处时已经参与到,m1、m2这个体系中的参与质量。同理m2的参与质量也这样计算。m’1、m’2成为一体就类似于地—月系统,太阳以它们的质量中心吸引它们。 如图2,M为太阳,m1、m2为内轨行星和外轨行星,O点为 m1、m2质量中心,m’1、m’2为两颗行星参与相互作用的参与质量,就是这两个行星彼此之间所产生的这个引力力度足可以使这两个行星上有m’1、m’2 这么大的质量彼此行成一体,类似地球和月球的关系。R1、R2分别为m1、m2到太阳的距离,R3为O点到太阳的距离,即两颗行星质量中心到太阳的距离,r1、r2为m1、m2到质量中心O的距离,r为m1、m2之间的距离。以质量中心O点为圆心作为一个球体圆,这个球体圆就是两颗行星之间所形成的微弱的质量中心到两颗行星之间的范围。在遥远处这个球体圆的中心点就是计算用的中心点,如地—月系统的地、月质心对太阳而言。那么太阳会使这个球体圆产生类似地球的潮汐现象,在球体圆的向日面和背日面可能都会产生隆起。那么两个行星在这个球体圆中同样要受到这一作用力。 两颗行星相会各自有多少参与质量主要取决于使它们能成为一体的临界线在什么位置,这条临界线确定了,参与质量也就确定了,那么它们各自的单独引力和在质量中心的引力也就确定了。所以最关键的就是确定这个临界线的位置。而实质上两颗行星是根本就不可能靠近而成为一体的,而且每两颗相邻行星都不相同,就是内轨行星和外轨行星也不相同,还有动能势能的转换、离心力引力的平衡等。那么这个临界线的位置就只能是设定、推演和推算。这个人们以后可以搞一个更好的推算方法。 如图3,这里做这样一个设定: m1、m2分别以r’1、r’2的距离在它们的质量中心的下、上位置,m1、m2所外延的引力场强度与太阳M在此处的引力场强度相同(有误差),即
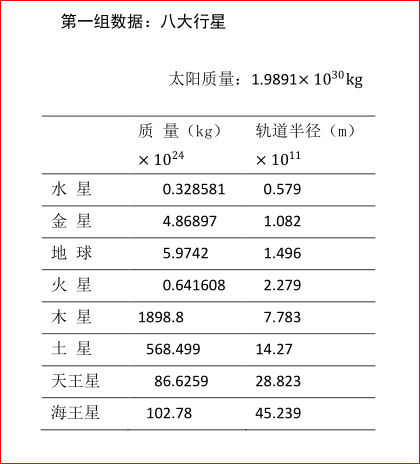
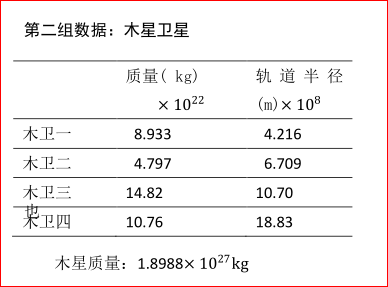
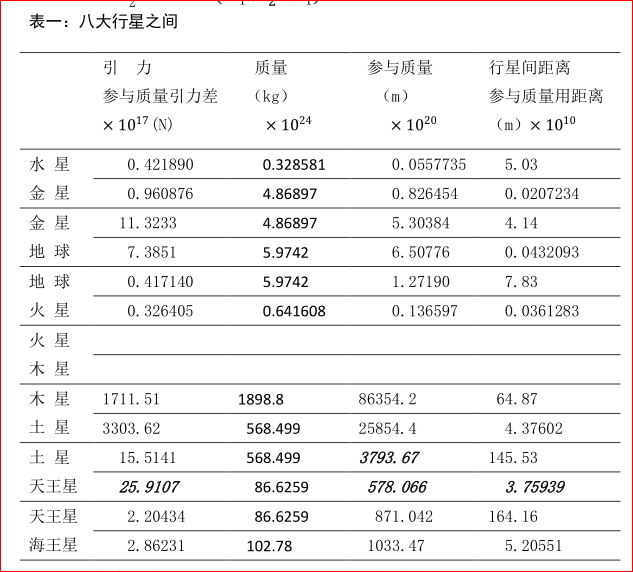
因为形成一个体系时和形成一个体系后差别很大。因为按这个设定计算,地—月间只有17万千米,而现实是38万千米。也有人研究认为“在月球形成后1~2亿年时,月球的最佳位置为24~27个地球半径file:///C:/Users/ADMINI~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.gif。”这里这样设定计算的结果与实际观测结果能吻合的好一点。当然还可以做其它一些设定。 如图2,m’1、m’2 是两颗行星在这个球体圆中相互作用的参与质量,这两个质量在球体圆两头和中心所受到的引力差。(这里不叫潮汐力,因为潮汐力是引力与离心力的合力,这里只是引力,暂时不包含离心力,这里是两颗行星互不相关时状态的叠加假设。)即: 用(8)式按上面的设定n=1计算两颗行星或两颗卫星之间的引力差,用 F=Gm1m2/r^2 计算两颗行星或两颗卫星之间的引力。用下面的二组数据对太阳系的八大行星及木星的四颗伽利略卫星做一下计算,结果如表一、表二。但这个计算值比实际值可能要大一点。 对以上的计算结果可以做的解释: 1、水星与金星的参与质量引力差很大。因为计算它们之间的参与质量引力差的条件已达到了极限,就是 r 2 近于 r’2,它们的质量中心太靠近金星了, R1 和r也相差很少。火星和木星的参与质量引力差没有计算,因为它们之间的条件已经超过极限了,就是file:///C:/Users/ADMINI~1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.gif 小于r’2了,它们的质量中心更近于木星的表面。这种条件已经构成了能成为一个体系(地—月系统)的条件了,但它们还不是一个体系的,怎样计算它们的参与质量引力差需要进一步讨论。本文的这种计算星体之间参与质量引力差的方法也不一定正确,只是揭示星体之间存在参与质量引力差的必然。对水星与金星的计算结果就不准确,它们之间的参与质量引力差具体是多少,应该在水星、金星下合时通过观测验证。但它们之间的分离是应该存在的,这可能是“水星总是向太阳方向掉一点”的原因或轨道进动的因素。 2、木星的四颗伽利略卫星都是参与质量引力差大于引力,木卫一有如水星,被推向木星。“他们发现1891年以来木卫一的轨道已向木星移动了55千米,而木卫二和木卫三则分别向外运动了125千米和365千米file:///C:/Users/ADMINI~1/AppData/Local/Temp/msohtmlclip1/01/clip_image004.gif。”如图4,木卫一转两周,木卫二转一周,它们总是在轨道相距最远处相会(上面),木卫一将木卫二轨道向上推。木卫二转两周,木卫三转一周,它们也是在轨道相距最远处相会(下面),木卫三又将木卫二的轨道再次向上推,所以木卫二的轨道偏心率大。木卫一转四周,木卫三转一周,它们三次下合,木卫三的轨道三次在120角度上被木卫一纠正。所以轨道偏心率小。 3、木星和土星相会时彼此远离,它们之间的参与质量引力差也确实远大于引力,这于观测相符。地球与金星、火星之间引力与参与质量引力差差别不大,所以下合是轨道没有多少变化,这也与实测相符。土星与天王星之间也是不符合计算条件的,因为r大于R1,不能成为两个相近的星体形成一个质量中心再对另外一个星体。但也计算了一下,在表中用黑斜字体表示,仅供参考。 如果地球上可以产生潮汐是一个鸭蛋,地—月系统就是一个软皮蛋,行星相会就是一个超级软皮蛋。本文讲的星体之间的参与质量引力差的作用力,不仅仅包含引力差的问题,主要是这个超级软皮蛋,它是起作用的,它不是实体但却起着实体的作用。在实验室用测定万有引力常数G的方法应该能测到这个软彼蛋的效应,这也有待于进一步探讨。
参考文献 [1] 陈宗镛《潮汐学》科学出版社 1980年 [2] 易照华《天体力学引论》科学出版社1978年6月 [3] 赵进义 编著 易照华 修订《天体力学》上海科学技术出版社1983年 [4] 维基百科网站 星友空间站 天之文、牧夫等网站
|