星体之间的潮汐作用

           星体之间的潮汐作用http://chiyang1234.blog.163.com/blog/static/1936666220154142421167/

姓名：       单位：                  邮政编码：

摘  要：对引力的一些不解之迷，如月球的运动等，是因为人们没有发现：星体与星体之间在存有第三星体的条件下会产生一种类似于地球上的潮汐现象的潮汐作用力。如太阳和八大行星之间，当两颗行星相会时它们的引力场会彼此构成一个虚球，两颗行星各自都有一部分质量参与到这个虚球中来并被潮汐力推动。这样两颗行星相会时就会表现出吸引、排斥、不吸引也不排斥的特征。这将揭开诸多引力之迷，对太阳系将有一个崭新的评估。

关键词：虚球   参与质量   潮汐现象    潮汐作用力

分类号：P

宇宙间存在万有引力，自牛顿发现并给出万有引力公式后，人们用这一公式解决了千千万万个问题，但随着观测精度和计算精度的不断提高，误差则不断的显露出来。这是人们还没有发现质量体与质量体、星体与星体之间在存有第三质量体和星体的条件下会产生一种类似于地球上的潮汐现象的潮汐作用。如行星和行星之间在太阳的作用下和卫星与卫星之间在行星的作用下都会产生一种潮汐作用。这一作用力较小时会减小两个行星之间及二个卫星之间的引力，较大时会使两个行星或二个卫星相互远离。这一作用力是未被人们发现的引力间的相互作用力。在过去的测定万有引力常数G和天体运行计算中都不包含它，所以必然存在不足。以后将精确测定万有引力常数G并从新计算太阳系星体的运行。这也将揭开一些关于万有引力的迷惑问题。

以行星和太阳为例，如图1，M为太阳，m1、m2为内轨行星和外轨行星，O点为 m1、m2质量中心，m’1、m’2为两颗行星参与相互作用的质量，R1、R2分别为m1、m2到太阳的距离，R3为O点到太阳的距离，即虚球中心到太阳的距离，r1、r2为m1、m2到质量中心O的距离，r为m1、m2的距离。以质量中心O点为圆心会形成一个虚球，在遥远处这个虚球的中心点就是计算用的中心点，如地—月系统的地、月质心对太阳而言。那么太阳对这个虚球必然会产生象太阳对地球一样的潮汐作用，在虚球的向阳面和背阳面都会潮汐隆起。那么两个行星在这个虚球中同样要受到这一潮汐作用力。

m1、m2 在不相遇时各自按照各自的轨道遵守引力与离心力平衡的规则绕太阳运行。当它们相会（下合）时必然要相互吸引，那么m2对 m1 的引力即是m1 从太阳那失去的引力，同理m1 对m2 的引力也相当于m2 从太阳那获得的同样大小的引力。准确计算要按椭圆轨道，两颗行星相会时内、外轨行星在各自椭圆轨道上的具体位置，而且每次相会时两颗行星在各自椭圆轨道上的具体位置都是不相同的，还有其它行星在扇面上的位置都是不同的及联珠的状况等。而且和地球上的潮汐作用力还不同，地球上的引潮力是正、背面对称的（向月面所受到月球的引力与背月面地球绕地—月质心旋转的离心力），行星之间的引潮力是不对称的，还有其它的不同之处等。这里按圆形轨道概略计算一下它们之间相会时在垂向上最大引潮力[1]，即潮汐作用力，两颗行星按质点算，即：

m’1、m’2 是两颗行星在这个虚球中相互作用的参与质量，这个质量在虚球中受到虚球的潮汐作用，即：

         没有虚球时M对m1、m2的引力是正常的，有虚球后就等于虚球把M对m1、m2的引力做了二次分配。

m1、与m2之间的潮汐作用力与引力之间存在着：

1、引力大于潮汐作用力时两颗行星会相互靠近，质量小的靠近的多，质量大的靠近的少。内轨行星轨道外延，外轨行星轨道内收。

2、引力等于潮汐作用力时两颗行星还按原轨道运行。

3、引力小于潮汐作用力时两颗行星会相互拉开距离。内轨道行星轨道内收，外轨道行星轨道外延。

        两颗行星在相互靠近的时候会产生共同的轨道外延，因为在纵向上（相会）：

简单表示为：A+B＞C ，即太阳对两颗行星的单独引力之和大于两颗行星质量在它们质量中心处时太阳对它们的引力。轨道外延时会一个外延的多，一个外延的少，这又会拉开它们之间的距离，而这种拉开距离又会阻止它们轨道外延，所以细节是很复杂的，但最终会找到一个平衡点。基于A+B＞C 的原则，两颗行星在相互远离的时候会使它们轨道内收，同理内收又会减小它们之间的距离从而阻止内收，最后找到平衡点。

这个轨道外延和轨道内收的值很小，这里暂时不计。现按圆形轨道和不计轨道外延与内收值，则m1、m2之间的潮汐作用力与引力之差必然等于太阳对m1、m2的引力与它们的离心力之差，即：

用（10）式计算两颗行星或两颗卫星之间的潮汐作用力。用下面的三组数据对太阳系的八大行星及木星的四颗伽利略卫星和火星的两颗卫星做一下计算[1]，结果如表一、表二、表三。但这个计算值可能比实际值要大一点。

从这些数据中可以看到；

表一的结果：

1、除火星、土星外其它行星都表现出对水星的吸引力，只有火星将水星推向太阳方向。其它行星对水星的引力因为有潮汐作用力的存在并没有人们以前计算的那么大。所以水星总是向太阳方向掉一点，这两点是主要原因。也应该从新计算水星的进动问题。勒威耶一定要寻找火神星，原来火神星就是火星其它行星和他脚下踩的地球。

1846年9月23日首次观测到海王星，当时海王星运行处于天王星之后并在一个稍大的角度上，如果它们表现是吸引的话海王星只能使天王星减速而不能使其加速，如果表现是潮汐作用力的话，由于角度较大作用力也是比较小的。但当时的木星和天王星正处于联珠半联珠状态（观测发现天王星加速到计算出来和观测到这还需要一段时间），也就是当时天王星的加速是木星对天王星的潮汐作用力的结果。正如后来人们发现勒威耶计算的轨道和海王星真实的轨道偏差很大，如果早几年或晚几年寻找海王星的话，根本无法在他所预测的位置找到它。勒威耶找到海王星是偶然的，找不到火神星是必然的。

这里木星对海王星的潮汐作用力最大，为：0.1956 N，而太阳对海王星的引力为：6.665 N。这个差距很严重，但前面谈过真实潮汐作用力要比这小。另外如果按参与质量的质量中心来计算，则是另一个结果，但在两者之间的结果是最理想的，但没有理论根据，这要在以后解决。

2、水星、金星和地球都在将火星推向木星方向，而木星和土星也都对火星表现出吸引力，所以火星在向木星方向靠拢，这在观测上已经得到证实；“海盗”1号、“海盗”2号着陆器以及“火星探路者”探测器上都有类似飞机上的无线电应答器，美国宇航局深空探测网可以测量这些着陆器和地球之间的距离，发现火星在远离地球。

3、水星、金星、地球都是相互吸引的，尤其金星和地球的引力很大，所以它们是相骤的。而木星对水星、金星、地球、火星也都是吸引的，所以类地行星在向木星靠近。观测证实天文单位正在以每世纪7米的速度增长。而类木行星间的强大的潮汐作用力也使木星向太阳方向靠拢。土星、天王星、海王星都表现出轨道外延，这与现在的观测也完全相符。木星和土星相会时的远离也是牛顿头痛的事，拉普拉斯以共振的理由解释缺少实据。星体的运行是由引力决定的，引力的综合决定星体怎样运行及共振，那么共振不能违反引力。

4、过去人们认为行星有恢复轨道的能力，实则是行星之间的引力没有人们计算的那么大，甚至彼此远离。这将从新估算太阳系的稳定性及演化趋势。看来任何三体都不是稳定的，最终都要演化成二体。类地行星与木星合一，其它类木行星飞走。但对银河系中心而言依然是三体。

表二的结果：

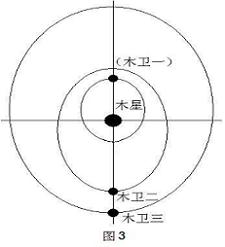
木卫一、木卫二分离，木卫二、木卫三吸引，木卫三、木卫四分离，这构成了分离、吸引、分离的阶梯。正是这种力的作用关系，使它们自1891年发现以来，木卫一轨道已向木星移动了55千米，木卫二和木卫三则分别向外移动了125千米和365千米[4]。

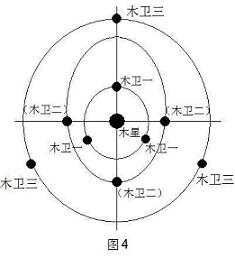
如图2，是木卫一与木卫二相会处及它们相会时木卫三所处的位置，由于它们是分离，内轨木卫一将处于近木星点，外轨木卫二将处于远木星点；如图3，是木卫二与木卫三相会处及它们相会时木卫一所处位置，由于它们是吸引，内轨木卫二将处于远木星点，外轨木卫三将处于近木星点；如图4，是木卫一与木卫三相会处及它们相会时木卫二所处的位置。木卫一与木卫二相会和木卫二与木卫三相会都是在椭圆的长半轴上，是由它们之间的潮汐作用力和引力决定的。因木卫一与木卫三的类似等边三角形的三点相会与它们之间的强大的潮汐作用力，它们的轨道会接近圆形，纠正了它们的椭圆形轨道，而木卫二没有得到这一纠正，所以木卫二的轨道扁率大。

伽利略卫星的共振只是这一潮汐作用力与引力在运行中找到的平衡点。作用力和反作用力必是对称的，平衡也一定在一个对称的条件下，它们在运行过程中、在周期和位置上具有对称的几何图形，因而形成这种运行规则就成为共振了。这个应该能计算出来。木卫四由于与木卫一、木卫二、木卫三的潮汐作用力而轨道外延，从而延长公转周期，在未来也将参与共振。

表三的结果：

现在观测已发现火卫一正在向火星靠拢，而火卫二正在远离火星，这与实际观测完全相符。

这个潮汐作用力很大，火卫一、火卫二应该以更大的尺度分离，而不是象现在观测到的以每世纪1.8米的速度分离。卫星轨道是近于圆形的，在相会时也是近于对称的，这个潮汐作用力也近似于保守力，所以它主要是改变卫星运行轨道的形状和进动等，德国女数学家诺特尔的理论：严格的对称对应严格的守恒，粗略的对称对应粗略的守恒。不对称的那部分力才是火卫一轨道半径减小火卫二轨道半径增大的力。

一、这个潮汐作用力对人造卫星的作用

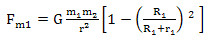
如图5，当m2、 很大时，即：  时，由（7）式 可知，对m1 的潮汐作用力最大。

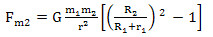
可知，对m2 的潮汐作用力近于零。如图6，当m2 很小，即  时，由（7）式可知对m1 的潮汐作用力近于零，由（8）式可知对m2 的潮汐作用力取决于 与 之比，也是最大值。但后者大于前者。也就是人造卫星处于向月面和背月面时的潮汐作用力是不相同的。但由于 与 、 比非常小，所以潮汐作用力对人造卫星是极小值。

二、月球运动理论中没有加入潮汐作用[2] [3]

地—月质心在地球半径的四分之三处，也就是 很小，这样太阳对月球的引力和太阳对月球的潮汐作用力差别很小，因而推导月球运动没有出现较大的误差。但是因为基点不对，虽然做了许多修正还是存在诸多不符。从根本上讲不存在太阳对地球和月球的单独引力，只存在太阳对地—月质心的引力和太阳对地球和月球的潮汐作用力。地、月是一个完整的体系，它们已经纠缠在一起了。太阳对地—月质心的引力是处理太阳与地—月质心之间的问题；太阳对地球和月球的引力是潮汐作用力，是处理地球和月球之间的问题，是一个体系的内部问题。

地—月系统是一个完整的独立系统，全部质量就是参与质量。如果没有虚球，则M对m1和m2 的引力为：

则潮汐作用力就是没有虑球和有虑球时M对 、 的引力差。

这一潮汐作用力会使地、月之间的距离加大。这里取一组地、月数据用（5）式概略计算一下地、月之间的潮汐作用力。

地、月是一个体系的，这个潮汐作用力是作用在一个体系内，不象行星与行星和卫星与卫星之间是作用在现两个体系上的。地—月还能自我灰复和调节，正如地球自我调节地球潮汐一样。但地—月间也不可能是正圆轨道，这潮汐作用力也不是保守力，也不可能完全左右对称，这不同于行星与行星和卫星与卫星之间。所以还是把它们拉远了一点点。太阳和月球并不能把地球拉成鸭蛋形，因为地球是转动的，如果地球不自转被潮汐锁定后则会成为鸭蛋形。因地—月系统围着太阳转，被拉的方向在不断调整，所以月球的轨道没有被拉长。

三、测定万有引力常数G必然出现误差

用扭称测G：测G是静态，不象行星和卫星是旋转的，不会形成潮汐隆起，但存在虚球，会以同样的量级减小两个质量体之间的引力，和前面地—月系与太阳的状况基本相同。静止状态的三个质量体在没有任何干扰的条件下能形成其中两个质量体的质量中心围绕另一个质量体旋转，这个静止状态的三体就可以按潮汐作用计算，其中两个质量体的全部质量都是参与质量。如用 2千克和 5千克的两个球相距0.2米来测量，在相距它们100米处有一个1000千克物体。则静止时相距近的两个球之间的潮汐作用力为：

前两项是只有M没有虚球时m1、m2 之间的引力差，而后一项是因有虚球才有的，无论m1、m2哪个大，都会使它们之间的引力减小。M对m1、m2的引力经过虚球的二次分配后也是不均衡的。

上式代入数据计算得F＝G0.00114N，而没有虚球时前两项之差是 N， G0.00114 N＝0.29886 N，显然误差就出来了，如是50米远，则F＝G0.009 N误差更大。

用两个原子重力仪上下排列，中间加重物进行变动测量也同样存在潮汐作用，如前所述。

只要是三体关系就存在潮汐作用，因为最起码要有仪器、重物和地球，也可能还会有上、下、远、近各处的其它物体。但也会有相互抵消的时候。因此测量万有引力常数G要选在平原而且地质环境好，重力异常平稳，自然环境平静没有干扰的地方，且建筑物要专门设计。

四、这一潮汐作用也在改变着双星的轨道

银河系所有的恒星都在围绕着银心旋转，银心对它们都有很大的引力，这个引力对双星所产生的潮汐作用力会影响它们之间的距离，会使它们的轨道变扁长。这个作用和太阳对地—月系统的作用一样。但双星互相围绕着旋转的速度快，银心对它们的潮汐作用要比太阳对地—月系统的作用重一些。双星绕银心转动的半径太大，转一周的时间太漫长，不象地—月系统一年转一周，轨道能得到及时调整。它们的轨道不能得到及时的调整，所以双星的轨道扁率都比较大。另外，同样的条件下质量差大的二体潮汐作用力小，质量差小的二体潮汐作用力大。双星的质量都比较接近或差别不是很大， 这也是双星与地—月系统的差别。

五、先驱者10号、11号的减速

引力理论证明一个球壳对球壳内的任一质点的引力等于零，对球壳外的任一质点的引力等于球壳质量集中在球壳中心对这一质点的引力。八大行星与太阳和八大行星之间也会形成一个一个的虚球，如图7，那么单独计算太阳和行星对质点的引力，则质点在虚球内所受到的虚球的引力是零，而在虚球外则受到相当于虚球中心的引力。飞船在突破和进入这些虚球的时候就会有微微的一点点的引力差别。当然这些虚球的组合是镶嵌的复杂的。但从远处长时间看应该是象行星的公转轨道一样以太阳为中心一层一层的外延至太阳系边缘。也就是对质点来说球壳外的引力必然大于球壳内的引力，因为在球壳外相当于八大行星所有的质量集中在球心对质点的引力，而在球壳内各行星的质量并不等于集中在太阳上，对质点来说某个行星会与质点成很大的角度，有的是反方向的，那么在单位尺度上按万有引力公式计算对质点的引力必然小了一点点。另外从远外看八大行星也将太阳的质量外延了一点点。

结束语

这里这些计算都是概略计算，公式也是去掉了所有的细节用了一个简单易明的式子，也没有算土星、天王星、海王星的卫星，因已算的这些对说明这一原理就已经够了。对于每一个计算结果都没有给出一个最终的定量结果，这是因为每一个定量结果都要涉及一个很大的范围，不是轻易定量的了的。还有行星之间、卫星之间联珠、半联珠的时候，力的作用会更复杂。这些具体的繁琐复杂的工作由专业研究者来做，我只是一个业余天文爱好者，目的是提出这一基本理论抛砖引玉，人们借此搞出一个更完好的理论解决天体力学中这些久有的疑难问题，使人类的科学正确的向前发展，走出这些泥潭，减少人们在这些问题上所花费的时间和精力，也节省人类的资源，对人类的未来—太阳系的稳定有一个准确的评估。

两颗行星相距很远相会那互相之间没什么作用，相距很近相会就成了地—月系统；相距不远不近相会则是在前两者之间，那么太阳对这种半地—月系统的引力作用一定具有对地—月系统引力作用的一部分内含。

有人在寻找万有斥力，在长程上不在微观内不存在斥力，这个引力间的潮汐作用力就算是万有斥力吧。

2014年11月14日