有關日食一點小知識

zhou_hao的理解比我要深，我开始只在平面的二维空间思考，zhou_hao已经在思考立体的三维空间了。

谢谢余老师

上午看了那本书...在月球近地点地球远日点时,本影锥的长度已经深入地球29449公里深了,足可以到两极了啊

刚才用EMAP查了一下,找到了2094年1月16日南极点的日全食...不知是否存在矛盾

[ 本帖最后由 zhou_hao 于 2007-3-24 14:08 编辑 ]

S O L A R     E C L I P S E     P R E D I C T I O N   for  2094 一月 16
                    Canberra, A.C.T., AUSTRALIA
East Longitude    5  0.00
      Latitude  -90  0.00
      Altitude   0 m.
        deltaT  106 secs

Event               UT        P.A.   alt.      Differential Corrections
                  h  m  s       o      o          A       B       C

First Contact    17 52 30     264     21         0.00    1.78   -0.01
Second Contact   18 47  6      46      
Maximum Eclipse  18 47 50             21         0.00    1.71   -0.01
Third Contact    18 48 34     303      
Last Contact     19 43 11      85     21         0.00    1.55    0.00

At Maximum Eclipse
Distance from Centre of eclipse    0.005593       0.0   -53.0 -145.38
             Shadow Radius   L2    -.009046
           Shadow movement    n    +.582204

Magnitude of Maximum Eclipse 1.034

好文，学习了。至于南北两极的问题，能有一个轨道图就更好了

有点疑惑呢，O版说的南北两极我看了半天才知道是南北极点。因为南北两极照道理来讲是南北极圈以上都是极地了。
2015年5月20日，日全食，日食轨迹几乎过北极点哦，没有达到90°。
不用等到2094年了，2094年也是没达到90°。
不过这两次纬度都超过了89°

点这个网址就再点2015那行就明白了。
http://eclipse.gsfc.nasa.gov/SEcat/SEdecade2011.html

值得好好一读，但我现在也对南北极点附近能否看到日全食搞不清了。从基本数据看，貌似能够看到的啊；不过真正要看到，还得计算一个整周期中每次的全食带吧。

Dear Dr. Yue and other fellows,
quite funny... i think 2-d is enough to take the question into account since we need to find a local max or min value or if we can't find it out, a reasonable value under extreme circumstances should be find out at least.

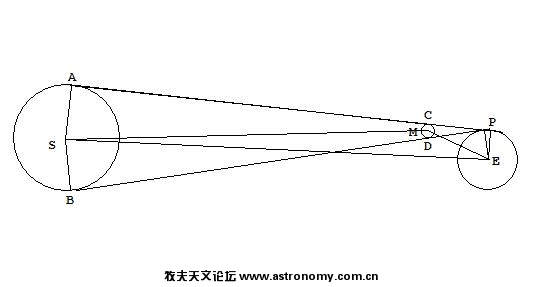
labels are shown in to illustration. MD = R_m = 384400 km, SB = R_s = 1.496*10^8 km, and < MES = 57m21s are all known; SM can be worked out according to the sine formula;  cos<BSM = (BS - MD)/SM, so <MSE can be worked out; hence we've <BSE = < BSM - < MSE.
MS = sqrt (SE^2 + ME^2 - 2*SE*ME*cos <MES) = 1.4922*10^8 km;
<BSM = 89deg44m0.99s; <MSE = 8.86s; => <SEP = <BSE = 89deg43m52.13s;
SE is parallel to ecliptic. (elongation 23deg27m) => central eclipse visible at two poles!? contradiction...  awaiting good explanation...
Cheers, Man-To Hui

[values' errors corrected]